Befreundete Zahlen
Zwei verschiedene natürliche Zahlen, von denen jeweils eine Zahl die Summe der positiven echten Teiler der anderen Zahl ist, bilden ein Paar befreundeter Zahlen.
Das kleinste befreundete Zahlenpaar wird von den Zahlen 220 und 284 gebildet. Die Summe der echten Teiler von 220 ergibt 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284 und die Summe der echten Teiler von 284 ergibt 1 + 2 + 4 + 71 + 142 = 220.
In einem befreundeten Zahlenpaar ist stets die kleinere Zahl abundant und die größere defizient.
Erstmals erwähnt wurden die Befreundeten Zahlen 220 und 284 von Pythagoras etwa 500 v. Chr. "Einer, der ein anderes Ich ist, wie 220 und 284."
1636 entdeckte Pierre de Fermat die befreundeten Zahlen 17296 und 18416, diese waren jedoch schon im 14. Jahrhundert von Ibn al-Banna und Kamaladdin Farist entdeckt worden. "Die Zahlen 17296 und 18416 sind befreundet, die eine abundant, die andere defizient. Allah ist allwissend." (Ibn al-Banna)
Errechnet werden können diese Zahlenpaare mit dem Satz von Thabit Ibn Qurrah:
- Für eine feste natürliche Zahl n sei x = 3·2n-1, y = 3·2n-1-1 und z = 9·22n-1-1.
- Wenn x, y und z Primzahlen sind, dann sind die beiden Zahlen a = 2n·x·y und b = 2n·z befreundet.
Leider liefert dieser Satz für n < 20 000 nur in den Fällen n = 2, n = 4 und n = 7 die erforderlichen drei Primzahlen. Heute ist bekannt, dass man mit dem Satz von Thabit keine weiteren befreundeten Zahlen für n ≤ 191600 ermitteln kann.
Leonhard Euler verallgemeinerte den Satz von Thabit:
- Für eine feste natürliche Zahl n sei
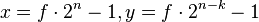 und
und  mit f = 2k + 1 und n > k > 0.
mit f = 2k + 1 und n > k > 0. - Wenn x, y und z Primzahlen sind, dann sind die beiden Zahlen
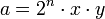 und
und 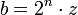 befreundet.
befreundet.
- Bei k=1 erhält man den Satz von Thabit.
2007 waren beinahe 12 Mio. befreundete Zahlen bekannt. Man vermutet, dass es unendlich viele befreundete Zahlen gibt, aber ein Beweis ist bisher nicht bekannt.
Weitere befreundete Zahlenpaare kann man mit Hilfe des Satzes von Walter Borho finden:
- Seien A und B befreundete Zahlen mit A = a·u und B = a·s, wobei s eine Primzahl ist, und sei weiter p = u+s+1 eine Primzahl und p kein Teiler von a.
- Dann gilt: Sind für eine feste natürliche Zahl n q1 = (u+1)pn-1 prim und q2 = (u+1)(s+1)pn-1 prim, dann sind A1 = Apnq1 und B1 = apnq2 befreundete Zahlen.
Mit Hilfe dieses Satzes fand Borho weitere 10.455 befreundete Zahlen.
Die Liste aller befreundeter Zahlen unterhalb von 10 000 000
| Nr. | erste Zahl | zweite Zahl | Jahr | Entdecker |
| 1 | 220 | 284 | - | Pythagoras(?)/Thabit |
| 2 | 1184 | 1210 | 1860 | Paganini |
| 3 | 2620 | 2924 | 1747 | Euler |
| 4 | 5020 | 5564 | 1747 | Euler |
| 5 | 6232 | 6368 | 1747 | Euler |
| 6 | 10744 | 10856 | 1747 | Euler |
| 7 | 12285 | 14595 | 1939 | Brown |
| 8 | 17296 | 18416 | um 1300/um 1300/1636 | Ibn-al-Banna/Farisi/Pierre de Fermat |
| 9 | 63020 | 76084 | 1747 | Euler |
| 10 | 66928 | 66992 | 1747 | Euler |
| 11 | 67095 | 71145 | 1747 | Euler |
| 12 | 69615 | 87633 | 1747 | Euler |
| 13 | 79750 | 88730 | 1964 | Rolf |
| 14 | 100485 | 124155 | 1747 | Euler |
| 15 | 122265 | 139815 | 1747 | Euler |
| 16 | 122368 | 123152 | 1941/42 | Poulet |
| 17 | 141664 | 153176 | 1747 | Euler |
| 18 | 142310 | 168730 | 1747 | Euler |
| 19 | 171856 | 176336 | 1747 | Euler |
| 20 | 176272 | 180848 | 1747 | Euler |
| 21 | 185368 | 203432 | 1966 | Alanen/Ore/Stempel |
| 22 | 196724 | 202444 | 1747 | Euler |
| 23 | 280540 | 365084 | 1966 | Alanen/Ore/Stempel |
| 24 | 308620 | 389924 | 1747 | Euler |
| 25 | 319550 | 430402 | 1966 | Alanen/Ore/Stempel |
| 26 | 356408 | 399592 | 1921 | Mason |
| 27 | 437456 | 455344 | 1747 | Euler |
| 28 | 469028 | 486178 | 1966 | Alanen/Ore/Stempel |
| 29 | 503056 | 514736 | 1747 | Euler |
| 30 | 522405 | 525915 | 1747 | Euler |
| 31 | 600392 | 669688 | 1921 | Mason |
| 32 | 609928 | 686072 | 1747 | Euler |
| 33 | 624184 | 691256 | 1921 | Mason |
| 34 | 635624 | 712216 | 1921 | Mason |
| 35 | 643336 | 652664 | 1747 | Euler |
| 36 | 667964 | 783556 | 1966 | Alanen/Ore/Stempel |
| 37 | 726104 | 796696 | 1921 | Mason |
| 38 | 802725 | 863835 | 1966 | Alanen/Ore/Stempel |
| 39 | 879712 | 901424 | 1966 | Alanen/Ore/Stempel |
| 40 | 898216 | 980984 | 1747 | Euler |
| 41 | 947835 | 1125765 | 1946 | Escott |
| 42 | 998104 | 1043096 | 1966 | Alanen/Ore/Stempel |
| 43 | 1077890 | 1099390 | 1966 | Lee |
| 44 | 1154450 | 1189150 | 1957 | Garcia |
| 45 | 1156870 | 1292570 | 1946 | Escott |
| 46 | 1175265 | 1438983 | 1747 | Euler |
| 47 | 1185376 | 1286744 | 1929 | Gerardin |
| 48 | 1280565 | 1340235 | 1747 | Euler |
| 49 | 1328470 | 1483850 | 1966 | Lee |
| 50 | 1358595 | 1486845 | 1747 | Euler |
| 51 | 1392368 | 1464592 | 1747 | Euler |
| 52 | 1466150 | 1747930 | 1966 | Lee |
| 53 | 1468324 | 1749212 | 1967 | Bratley/McKay |
| 54 | 1511930 | 1598470 | 1946 | Escott |
| 55 | 1669910 | 2062570 | 1966 | Lee |
| 56 | 1798875 | 1870245 | 1967 | Bratley/McKay |
| 57 | 2082464 | 2090656 | 1747 | Euler |
| 58 | 2236570 | 2429030 | 1966 | Lee |
| 59 | 2652728 | 2941672 | 1921 | Mason |
| 60 | 2723792 | 2874064 | 1929 | Poulet |
| 61 | 2728726 | 3077354 | 1966 | Lee |
| 62 | 2739704 | 2928136 | 1747 | Euler |
| 63 | 2802416 | 2947216 | 1747 | Euler |
| 64 | 2803580 | 3716164 | 1967 | Bratley/McKay |
| 65 | 3276856 | 3721544 | 1747 | Euler |
| 66 | 3606850 | 3892670 | 1967 | Bratley/McKay |
| 67 | 3786904 | 4300136 | 1747 | Euler |
| 68 | 3805264 | 4006736 | 1929 | Poulet |
| 69 | 4238984 | 4314616 | 1967 | Bratley/McKay |
| 70 | 4246130 | 4488910 | 1747 | Euler |
| 71 | 4259750 | 4445050 | 1966 | Lee |
| 72 | 4482765 | 5120595 | 1957 | Garcia |
| 73 | 4532710 | 6135962 | 1957 | Garcia |
| 74 | 4604776 | 5162744 | 1966 | Lee |
| 75 | 5123090 | 5504110 | 1966 | Lee |
| 76 | 5147032 | 5843048 | 1747 | Euler |
| 77 | 5232010 | 5799542 | 1967 | Bratley/McKay |
| 78 | 5357625 | 5684679 | 1966 | Lee |
| 79 | 5385310 | 5812130 | 1967 | Bratley/McKay |
| 80 | 5459176 | 5495264 | 1967 | Lee |
| 81 | 5726072 | 6369928 | 1921 | Mason |
| 82 | 5730615 | 6088905 | 1966 | Lee |
| 83 | 5864660 | 7489324 | 1967 | Bratley/McKay |
| 84 | 6329416 | 6371384 | 1966 | Lee |
| 85 | 6377175 | 6680025 | 1966 | Lee |
| 86 | 6955216 | 7418864 | 1946 | Escott |
| 87 | 6993610 | 7158710 | 1957 | Garcia |
| 88 | 7275532 | 7471508 | 1967 | Bratley/McKay |
| 89 | 7288930 | 8221598 | 1966 | Lee |
| 90 | 7489112 | 7674088 | 1966 | Lee |
| 91 | 7577350 | 8493050 | 1966 | Lee |
| 92 | 7677248 | 7684672 | 1884 | Seelhoff |
| 93 | 7800544 | 7916696 | 1929 | Gerardin |
| 94 | 7850512 | 8052488 | 1966 | Lee |
| 95 | 8262136 | 8369864 | 1966 | Lee |
| 96 | 8619765 | 9627915 | 1957 | Garcia |
| 97 | 8666860 | 10638356 | 1966 | Lee |
| 98 | 8754130 | 10893230 | 1946 | Escott |
| 99 | 8826070 | 10043690 | 1967 | Bratley/McKay |
| 100 | 9071685 | 9498555 | 1946 | Escott |
| 101 | 9199496 | 9592504 | 1929 | Gerardin/Poulet |
| 102 | 9206925 | 10791795 | 1967 | Bratley/McKay |
| 103 | 9339704 | 9892936 | 1966 | Lee |
| 104 | 9363584 | 9437056 | um 1600/1638 | Yazdi/Rene Descartes |
| 105 | 9478910 | 11049730 | 1967 | Bratley/McKay |
| 106 | 9491625 | 10950615 | 1967 | Bratley/McKay |
| 107 | 9660950 | 10025290 | 1966 | Lee |
| 108 | 9773505 | 11791935 | 1967 | Bratley/McKay |
Quellen: http://de.wikipedia.org/wiki/Befreundete_Zahlen; http://www.mathe.tu-freiberg.de/~hebisch/cafe/vollkzahlen.html